本文讲解前端如何实现加入购物车动画,以及实现过程中的数学原理。
背景
在最近的一次前端项目中,需要实现加入购物车的抛物线动画,然后实现抛物线动画的过程中,发现原来当初学习的数学知识是有实践作用的,因此记录下来此次的心得与体会,望与大家共勉,感谢。
前端加入购物车动画的实现
我们的目标是实现加入购物车动画,为何要有动画效果,让操作能实现流畅的过渡,更自然。也让用户减少可能的焦躁。
在前端实现这个效果主要有以下两种实现方式。
利用嵌套元素线性叠加平移动画实现
直接从互联网搜索如何实现购物车动画,约90%的搜索结果都是使用这种方式实现的。
<div class="box">
<div class="content">
<div class="inner"></div>
</div>
</div>
.box {
width: 400px;
height: 400px;
background-color: #eee;
margin: 0 auto;
display: flex;
justify-content: flex-end;
}
.content {
width: 30px;
height: 30px;
border-radius: 50%;
background-color: #fff;
}
.inner {
width: 30px;
height: 30px;
border-radius: 50%;
background-color: #f0f;
}
上面一个嵌套元素的场景, .content 元素包裹着 .inner 元素,如果我们在鼠标悬停时候给 .content 元素增加沿X轴平移-300px的动画,并且给 .inner 元素增加沿Y轴平移300px的动画,那么这时候 .content 元素和 .inner 元素分别的运动轨迹是怎样的呢?
/* 增加平移动画 */
.content {
margin:30px;
width: 30px;
height: 30px;
border-radius: 50%;
background-color: #fff;
transition: all 1s linear;
}
.inner {
width: 30px;
height: 30px;
border-radius: 50%;
background-color: #f0f;
transition: all 1s linear;
}
/* 鼠标悬停效果 */
.content:hover {
transform: translateX(-300px);
}
.content:hover .inner {
transform: translateY(300px);
}
我们会发现 .content 元素会向左平移,符合预期,但 .inner 元素往左下斜线运动了,为什么会产生这种视觉效果呢?
-
嵌套的元素位移:
.inner是.content的子元素,他的位置是相对于.content的 。且.content在向左移动的同时,.inner也会随之向右移动。 -
位移的线性叠加:
.inner本身还有一个单独的translateY操作,它会在.content向左平移的过程中相对向下平移。因此,.inner的运动路径形成一个组合运动——既向左又向下,看起来像是在做“斜向的运动”。
但是现在的实现效果与我们的预期存在差别,现在 .inner 元素是斜线向下的,但现在生活中物体的运动存在惯性与引力的影响,斜线向下的过渡动画不真实自然,运动轨迹应该是曲线的,也就是曲率不能为0.
那么这种情况下如何将线性叠加的斜线运动变为曲线呢,这时候我们就会使用到 transition-timing-function , transition-timing-function 可以设置元素过渡动画的变化“速率”,我们把 .inner 的 transition-timing-function 设置为相对于线性先慢后快,就会形成看起来像是在做“斜向的抛物线运动”的线性叠加效果。
...
.inner {
width: 30px;
height: 30px;
border-radius: 50%;
background-color: #f0f;
transition: all 1s cubic-bezier(.51, .1, .78, .4);
}
...
那为什么 cubic-bezier(.51, .1, .78, .4) 是表示一个相对于 linear 会显得速度是先慢后快呢?
我们前端实现动画可以使用 cubic-bezier动画配置网站 找自己需要的变化“速率”函数。
函数曲线的斜率变化决定了函数变化的快慢,斜率如何求,这里我们只需要看函数切线与x轴的正切值 tan。也就是看图!
线性函数,斜率是tan45°,也就是恒定为1. 而查看 cubic-bezier(.51, .1, .78, .4)曲线的斜率不均匀,初始部分斜率比线性小,意味着起始速度较慢;中间部分斜率慢慢变大,速度增加;到最后部分斜率再次增加,速度越来越快。
- 初始阶段:时刻t=0: 斜率 ≈ 0.20
- t=0.25: 斜率 ≈ 0.51
- t=0.5: 斜率 ≈ 1.02
- t=0.75: 斜率 ≈ 1.78
- t=1: 斜率 ≈ 2.73
cubic-bezier(.51, .1, .78, .4) 是表示一个先快后慢的缓动曲线。
· 初始阶段:曲线的斜率较大,表示运动开始较快。
· 后半部分:曲线逐渐趋平,斜率减小,表示运动逐渐减速。
了解了三次方贝塞尔函数的作用以及如何看变化的“速率”,相信大家后面就能根据自己的场景结合 cubic-bezier动画配置网站 找适合自己的变化函数。
上面例子的完整代码 嵌套元素线性叠加动画示例代码demo 。
利用抛物线方程实现
上面的线性叠加实现,还是存在缺点的,例如现在需要运动先往上抛,然后再往下,上面的线性叠加方案就比较难实现了。
我们先想象先往上抛,再往下是怎样的.如图,坐标轴零点是物体出发点。
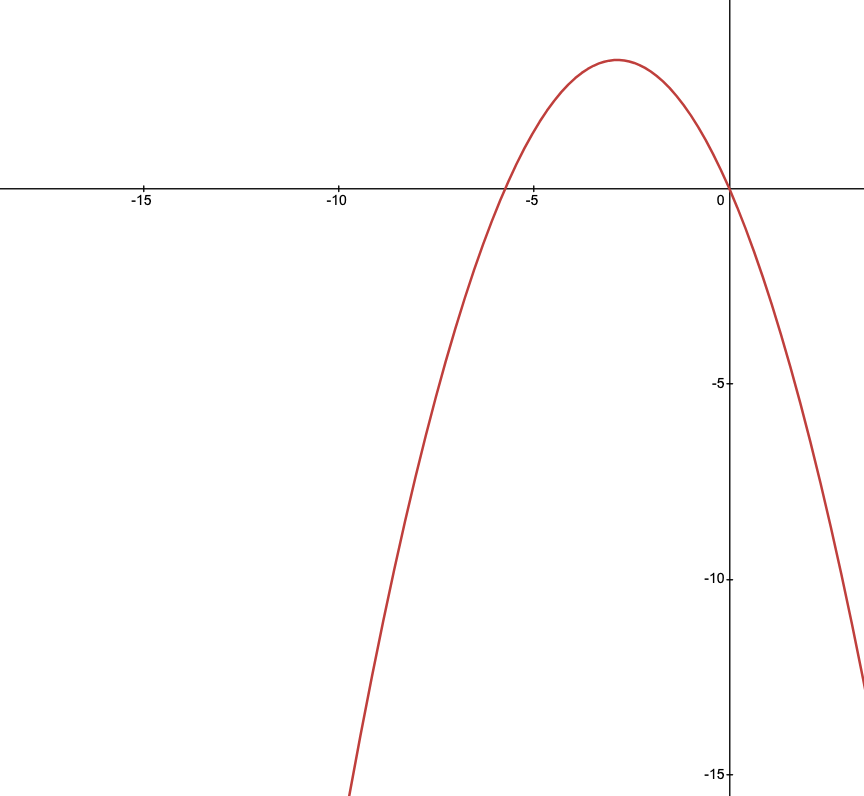
拆分元素的运动轨迹,我们可以先得出元素的x坐标是往左边均速变化(在前端与鸿蒙的过渡动画坐标轴是X轴坐标匀速变小)。
现在我们已知开始点(0,0), 终点(x0,y0). 假设我们需要在1秒内完成抛物线动画,可以根据速度 speedx = x0 - 0 / 1000 . 计算任意运动时刻下x轴的坐标。
那么y轴的坐标呢?
y轴的坐标是一条抛物线,这时候需要我们拾起初中数学学过的抛物线标准方程。
$y = a * x * x + b * x$
那么我们就可以设运动中的时刻为 t , 在该时刻下运动物体的横坐标 x 和纵坐标 y 可以使用下面的函数计算。
$x = speedx * t$
$y = a * x * x + b * x$
a、b、c是常数,我们先计算它们,运动会过坐标原点(0,0),所以得出 c 为 0. 这时候求y的方程式函数就变成了 $ y = a * x * x + b * x $.
然后我们再理解一下常数 a 的数学意义, a 控制抛物线的“弯曲”程度. 可以使用函数模拟网站形象地看出这个意义。
- 较大的 a 值:抛物线更“陡峭”,即元素会较早上升,然后快速下降。
- 较小的 a 值:抛物线较平缓,元素的上升和下降过程较为平滑。
实际我们编写代码的过程中可以通过实验调整 a 的值,达到最佳视觉效果, 这里我们暂时把 a 设为 0.004 .
已知a, 将终点(x0,y0) 代入方程式,我们可以计算出常数 b.
$b = (y0 - a * x0 * x0) / x0$
这样我们通过暂定 a 值,就可以计算出常数 a、 b、 c 了。
最后我们只需要将任何时刻 t 的 x 代入,就能得到该时候的纵坐标 y 了。
这时候我们可以使用前端的 requestAnimationFrame 来根据用户屏幕的频率不断地回调动画,计算任意时刻下小圆球元素的坐标点,然后移动小圆球元素来实现抛物线动画效果了。
具体的实现代码可以参考利用抛物线方程实现小球抛物线demo。
触类旁通的其余方法
可能初中数学课本学到的抛物线方程并不能满足各位本科学士,是否有其他方程式已知x轴坐标,求抛物线运动过程中的y轴坐标的?
方法是有的,那就是插值: 已知有限的若干个点,通过简单函数P(x)来代替原函数f(x),来近似真实情况,求出其他点的映射。
具体的应用可以使用贝塞尔曲线插值、牛顿插值、拉格朗日插值计算 y 的某个时刻的坐标。
篇幅有限,具体的使用,这边就不详谈,有兴趣的可以研究,我这边也提供一个使用拉格朗日插值计算抛物线小球运动轨迹的demo 。
总结
通过一次商品加入购物车的实践,讲述了如何实现并讲解了其中涉及的数学原理,希望能对大家有所启发,感谢。